Team:Pittsburgh/Model


The Kinetics of Split-inteins


Inteins exist in several classes which each have a slightly different splicing pathway. While splicing involves multiple steps, the final step (breakdown of the branched intermediate) is rate limiting and therefore we can model intein splicing as a pseudo first-order reaction.

Figure 1 Intein splicing can be modeled as an irreversable first-order reaction.

If we want to model split-inteins, we need to consider the association and disassociation constants. Therefore, we extend our model to include unbound precursor fragments as well as a bound complex.

Figure 2 A split-intein must first associate before it can splice. We model the association with two new rate constants: K_on and K_off. Once the bound complex has formed, it can splice to form the activated extein and excised intein.

ODE models


Using the reaction pathway given above, we can model intein splicing as a system of ordinary differential equations. We implemented this system in Python using scipy's "odeint" function to numerically integrate the system.

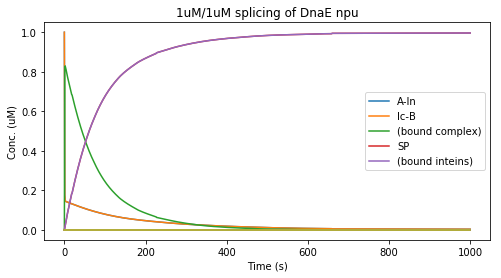
For a first test, we took rate constants for DnaE npu found in the literature [Shi 2005]:

  • K_on = 6.7 x 107 M-1 s-1
  • K_off = 1.7 s-1
  • K_splice = 1.4 x 10-2 s-1

We set the initial concentrations at 1uM of each split intein construct and integrated the concentrations over time:

Figure 3 Stochiometric intein reaction modeled with an ODE system. The equilibrium lies heavily towards the bound complex so it builds up initially and then is consumed in the splicing reaction. (A-In: N-terminal intein with extein, Ic-B: C-terminal intein with extein, SP: spliced product)

Non-stochiometric reactions


During our design process, we were conserned about our ability to experimentally control intein concentrations in our assay. We wanted to figure out if mixing inteins in non-stochiometric ammounts would severly limit the reaction rate and yield.

We used our simple ODE model to evaluate different starting conentrations as follows:

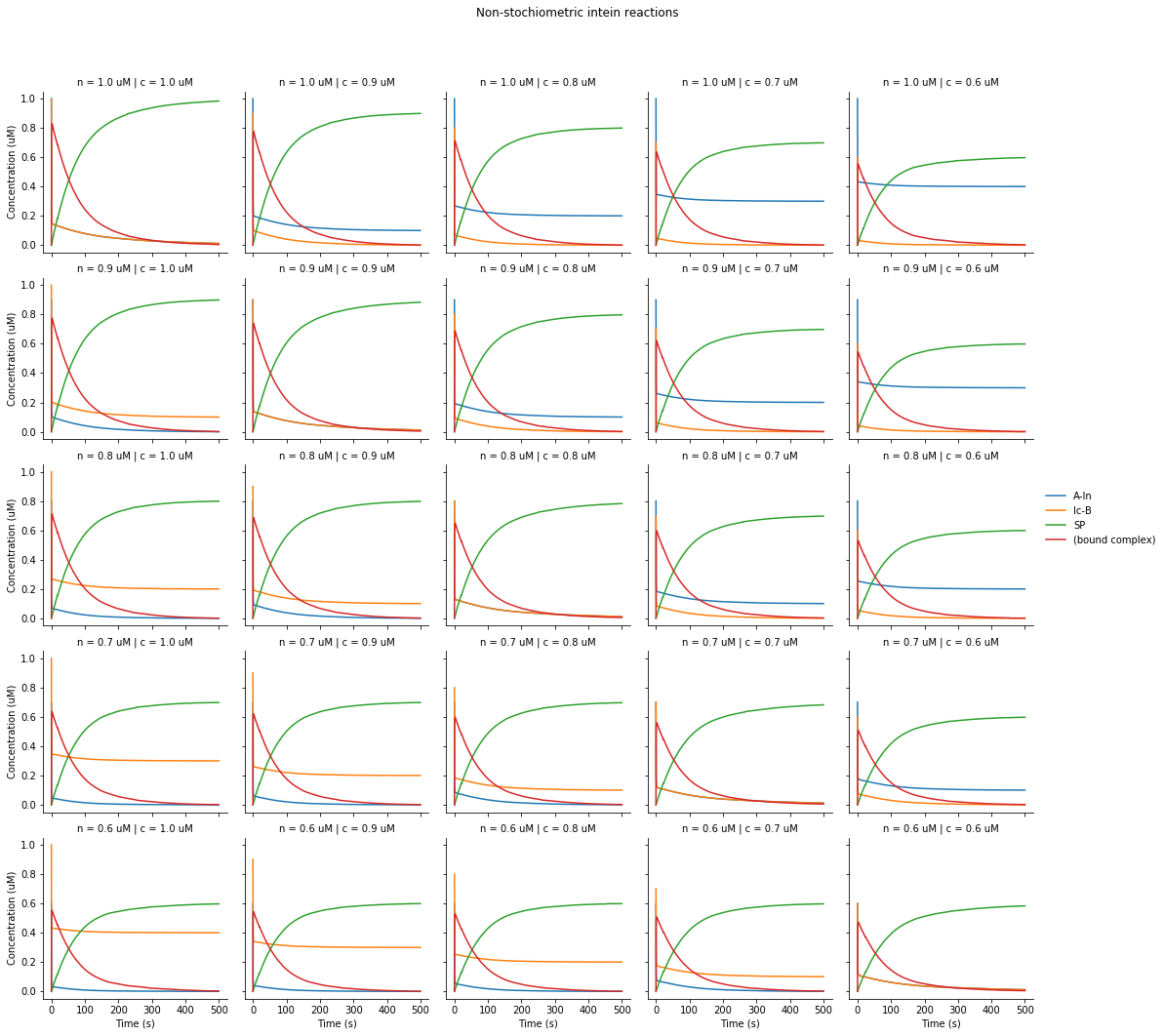
Figure 4 Non-stochiometric intein reaction modeled with an ODE system. Each subplot has a different starting concentration of N and C.

From this data, it appears that changing the starting concentrations affects the yield but not intein half-life. Therefore, it was not too much of a concern during our experimental setup.

Split-linker system


During the design phase of our split-linker system, we realized that the starting reactants can react to form a plethora of different intermediate reactants. Some of these reactants can no longer react with each other. We were concerned that a buildup of these products would hider the reaction and inhibit formation of the final spliced product.

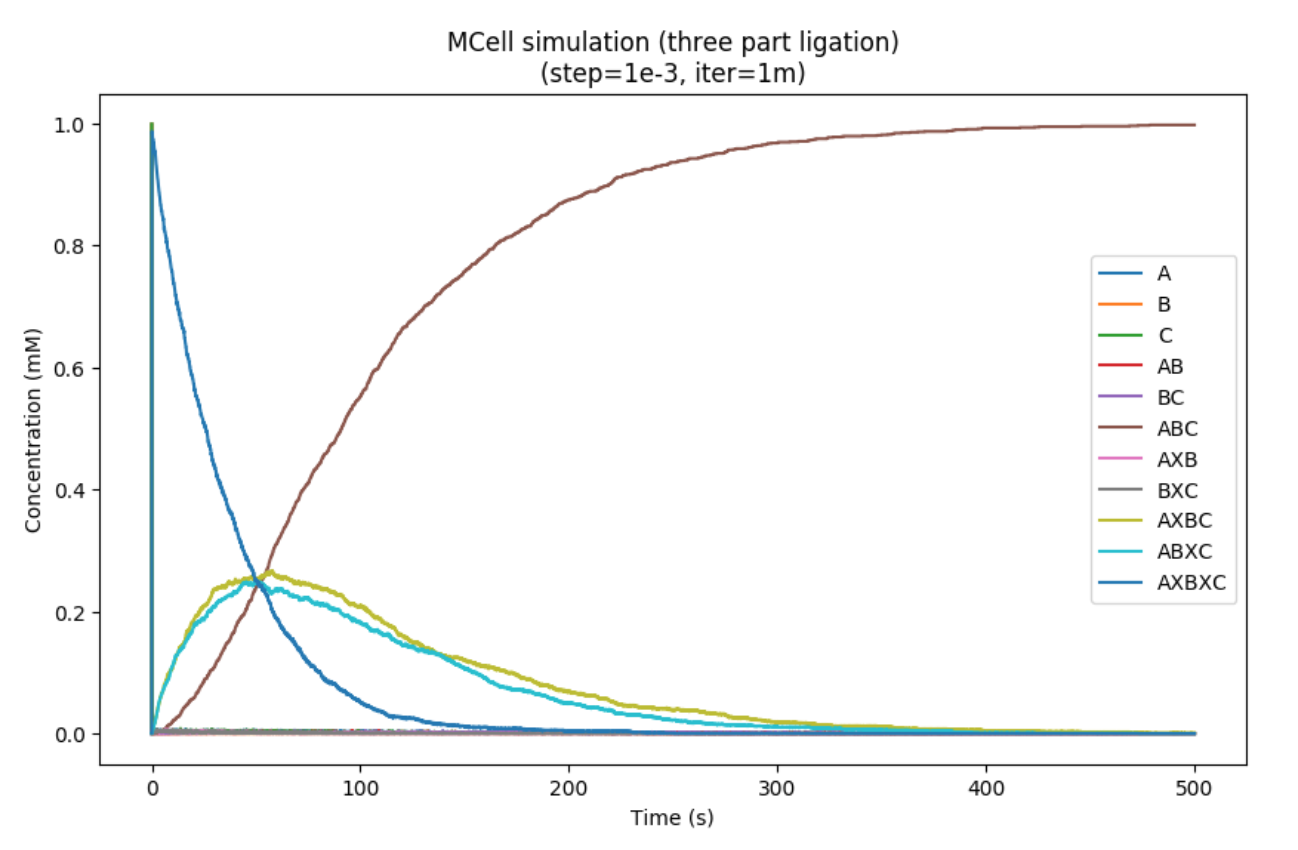
In order to test this idea, we built a monte-carlo simulation with MCell that stochastically simulates reaction mechanics. We are primarily concerned with multi-part ligation products. In order to model this system, we made the assumption that a construct with two fused inteins (such as the linker constructs) could associate to both of it's partners before either splices.

In three part ligation, we define three fragments: A,B and C. These fragments will splice to form ABC. However, before splicing, the inteins must associate. We represent this with an "X", for example "AXB" indicates the association of fragments A and B before splicing has occured. This construct could splice to form "AB" or associate to "C" forming "AXBXC". Additionally, it could disassociate back into "A" and "B".

The results of our three-part are below:

Figure 5 Monte-carlo three-part ligation simulation. We observe one initial "bump" containing single-spliced intermediate products. However, these quickly splice to form the doubly-spliced final product.

Additionally, we tried this simulation with a larger four-part splicing reaction:

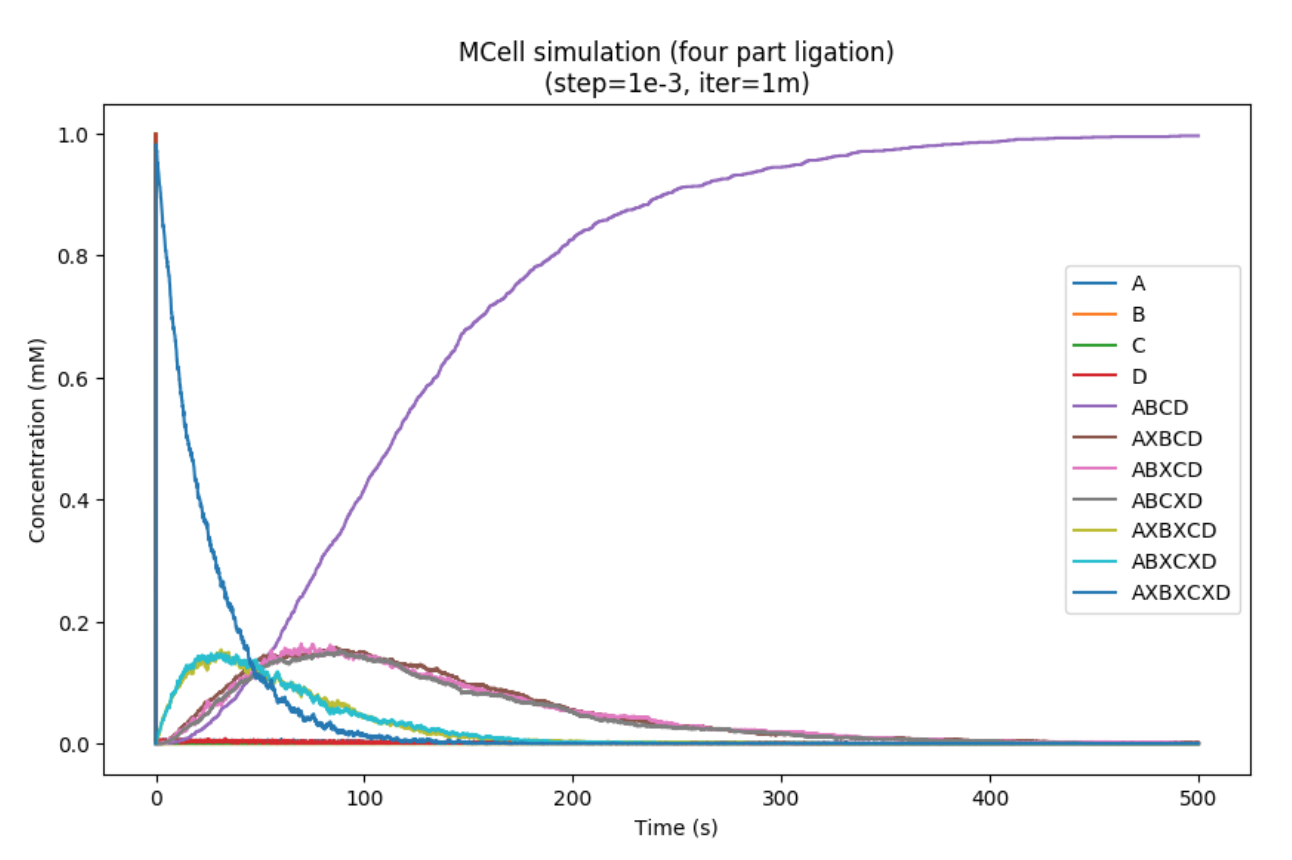
Figure 5 Monte-carlo four-part ligation simulation. Here we observe two bumps form, the first contains single-spliced intermediate products. The second bump contains double-spliced intermediate products.

Somewhat surprisingly, these models demonstrate that despite the formation of intermediate products that can't react with each other, the overall reaction rate is not hindered in a multi-part ligation reaction. One observation is that these intein splicing events do not depend on the state of the system and therefore can be considered independent events. Therefore, this four-part splicing model is equivalent to three splicing reactions operating in parallel.

A more detailed model of split-intein kinetics


During our research we observed many papers cite yields of 80-95% for split-intein reactions. However our simple intein splicing model predicts yields of close to 100%.

One idea for the observed low yields is that excised split-intein fragments bind to the starting material and form unproductive bound complexes. This idea is illustrated below:

Figure 6 Top: standard intein splicing model. Bottom: interference theory (with Inc-C excised intein). (not shown: symmetrical interference theory for Int-N excised intein) After intein splicing, the split inteins are excised from the host protein. However, at this stage they are not covalently bound and may disassociate (not shown). We hypothesize that excised split-intein fragments will associate with their cognate partner and form unproductive (catalically-inactive) bound complexes thereby lowering the concentration of available starting material.

This model has not been discussed in literature and therefore, we have no experimentally determined binding constants for excised inteins. However, the excised inteins have little chemical modification and therefore we would expect them to behave like non-excised inteins with regard to binding affinity. Therefore, we reused the same rate constants K_on and K_off to model excised intein association and disassociation.

Our model demonstrates a buildup of unproductive bound complex that inhibits the reaction yield:

Figure 7 Left: simple intein model (SP overlaps bound inteins). Right: interference model (both unproductive complexes appear in equal concentrations).

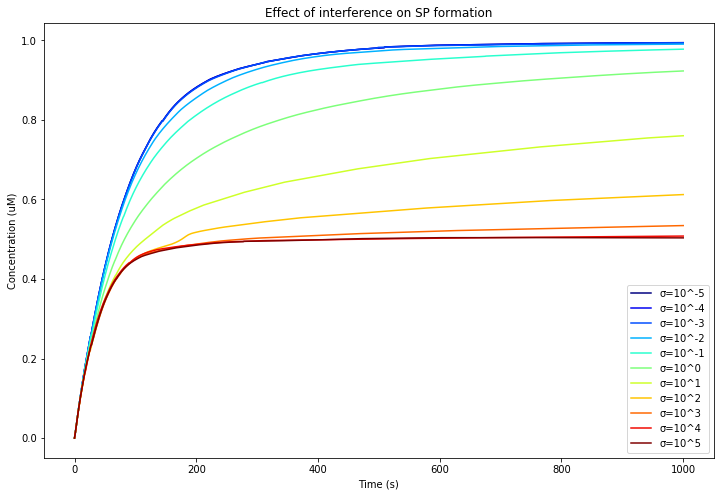
After speaking with Dr. Hideo Iwai, we learned about extein dependency - the effect of fused exteins on intein association. Since the excised inteins no longer have an extein, their "interference" association likely obeys a different rate constant. In order to explore this concept, we propose an association factor σ as a coefficient of on and off rates for interference association.

When σ = 1, the excised inteins have the same affinity as non-excised inteins. When σ < 1, the excised inteins have a weaker affinity and interference has less of an effect. When σ > 1, the excised inteins have a higher affinity and interference has more of an effect.

We can plot the formation of SP over time as a factor of σ:

Figure 8 Effect of excised intein affinity (σ) on the formation of spliced product (SP). With high values of σ, yield approaches a limit of 50%. With low values of σ, the yield approaches 100%.

Visual modeling


In the early stages of our research, we were seeing a lot of block diagrams to represent different intein reactions. This method of illustration warped our perception of what inteins actually look like and how they work.

For example, one concept that was not intuitive was that fusion proteins could be attached to both sides of a split intein without sterically hindering the reaction. Once we discovered the solubility issues with our nested intein constructs, we were able to use this new intuition to design fusion constructs with MBP that improved stability of our constructs.

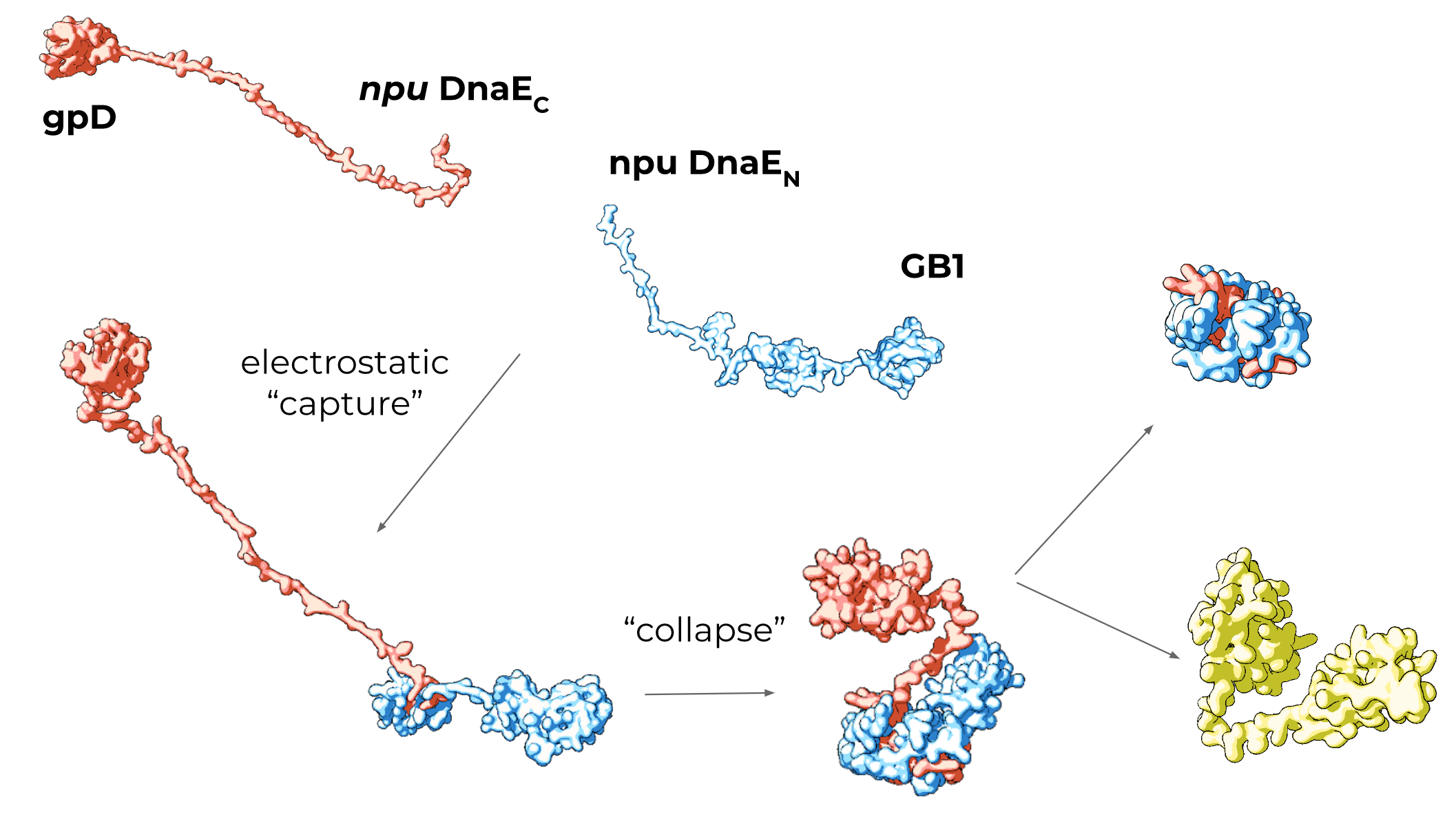
Inteins are intrinsicaly disordered proteins that assemble through electrostatic interactions and form a cis-like conformation before splicing. [Shah 2013] This disorder makes it difficult (if not impossible) to obtain crystal structure data of independent split inteins.

In order to obtain rough structural predictions of split intein fragments, we sourced structural data for GB1, gpD and the DnaE npu bound complex. Then, using Molecular Maya (a plugin for Autodesk Maya), we fused structural information from experimental data and filled in regions with no structural information. Using the inbuilt modeling toolkit, we arranged the protein structures in a potential conformation according to our understanding of association mechanics.

Our illustrated intein structures are below:

Figure 9 Intein fragments prior to association. Blue: (DnaE npu N)-GB1, Red: gpD-(DnaE npu C). The C intein domain is intrinsically disordered and the N intein domain is partially folded.
Figure 10 Intein fragments associate through electrostatic interactions and begin to collapse.
Figure 11 Intein fragments collapse into the bound complex. This conformation mimicks that of a cis-intein.
Figure 12 After splicing, the extein domains are covalently attached.
Figure 13 After splicing, the inteins are excised and remain bound through non-covalent interaction.
Figure 14 Full pathway of intein association and splicing.

How accurate are these visual models?


These models are artistic representations of intein fusion structures. The primary sequences are correct and most of the structural information is sourced from real experimental data. However, for regions with unknown (or intrinsically disordered) structure such as the pre-association intein fragments, we guessed at potential large scale conformations and allowed Molecular Maya to stabilize to a low-energy conformation.

These diagrams are intended to give the viewer an intuitive understanding of what split-inteins "look like" and how they associate. They are not experimentally derived however, and should not be misunderstood for scientific data.

References


[Shah 2013]

Shah, N. H., Eryilmaz, E., Cowburn, D., & Muir, T. W. (2013). Naturally split inteins assemble through a "capture and collapse" mechanism. Journal of the American Chemical Society, 135(49), 18673-18681. https://doi.org/10.1021/ja4104364

[Shi 2005]

Shi, J., & Muir, T. W. (2005). Development of a tandem protein trans-splicing system based on native and engineered split inteins. Journal of the American Chemical Society, 127(17), 6198-6206. https://doi.org/10.1021/ja042287w