Introduction
Our model simplifies the complex mechanism behind the sugar consumption hierarchy in E.coli to a basic enzymatic competitive inhibition model. Almost all sugar specific operon promoters are regulated by the same sensor, and by a specific sugar detection protein.
If the E.coli bacteria need energy, their cAMP levels rise and activate a sensor called CRP which will bind strongly to a strong sugar degradation operon (i.e lactose). If lactose is present, the production of proteins in its degradation pathway is enhanced, if not the E.coli does not produce them; however it still needs energy to grow ! cAMP levels continue to rise and continue to bind to CRP, increasingCRP’s affinity for the next, weaker promoter in the hierarchy (i.e Arabinose).

Once we determined all the “parameters" of the reaction, i.e CRP affinity for each promoter and the inhibition constant for the “weaker” promoter when a “stronger” promoter is active (AMP rises so cAMP decreases...), and plotted the experimental results into the appropriate graph, we had our model!!
1 - Simple promoter construct ( Monod Equation )
Our model is based on empirically defined equations, and we have modified them to integrate the parameters that interest us.
We will start by modeling the volume of the bacterial culture, Vculture :
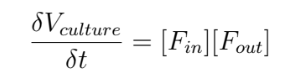
Where [Fin] = the total fluxes coming in to the culture.
And [Fin] = the total fluxes going out of the culture.
In the case of an isolated or “closed” culture, the fluxes [Fin] and [Fout] have a value of 0.
The next step is to modelize the cell growth and increase the precision of this model by taking into account the number of living cells (Xv) :

with u the number of cells and kd the number of cells that die per unit of time (constant). u varies in function of the amount of sugar available in the culture medium :

This equation strongly resembles that of Michaelis-Menten, with Umax and Ks that are constants and [S] that we will define further on.
Umax corresponds to the maximal number of cells during the stationary phase and Ks is the half-rate of
cell growth.
[S] corresponds to the concentration of sugar in the medium and will depend on the volume of the bacterial culture Vculture, on the culture medium and on the sugar consumption by the bacteria.

Q corresponds to the sugar consumption of 1 bacteria that we multiply by the number of living cells. It evolves depending on 2 factors : the minimum sugar consumption of the bacterium, m and the sugar consumption necessary to maintain the growth rate, Yx.

So far, we have modelized bacterial growth, for the next step we simply added the activation of a promoter by assuming that it operates in the same way, the cells consume sugars and these sugars allow the activation of our promoters of interest. So there
will not only be a link between a specific sugar consumption and the bacterial growth, but also with the activation of the sugar associated promoter.
Now we will focus on the sugar consumption of the cell. The enzymes responsible
for the degradation of these sugars are placed under the control of identified promoters that are activated by these same sugars. So if we assume that there is no delay between the activation of these promoters and the production of the degradation-enzymes,
we could study the activation of these promoters by studying the sugar-consumption by following the bacterial growth model : the more sugar consumed, the more the promoter associated to this sugar is activated. And from there, we can apply
the same model with a slight change :

2 - Double promoter construct
This is where it becomes slightly more complicated. We must now take into consideration that we are no longer studying 1 sugar associated promoter, but 2, therefore we need a model that takes 2 different sugars into account :

We must take into account that Ks1 and Ks2 are not equal to the Ks of a single sugar. To grow, the bacteria needs energy, that can be found in the sugar of the medium. However, the bacteria will not consume 2 sugars at the same rate as it would a single
sugar. The evolution of the sugar concentrations in the medium follow the same type of decrease as before. However, the values of Yx and m associated to each sugar will be smaller, due to a lower consumption of 1 specific sugar at a time.
Finally, the activity of the promoters should resemble the activity in the simple construct, however we will need to modelize the suppression of one promoter on the other, which will take form as the following term as a denominator


